FASES EN LA CONSTRUCCIÓN DEL MODELO

Cuando la suposición de normalidad no es adecuada o la relación lineal que se asume entre $X$ y $E(y|X)$ no es directa, se utiliza una extensión del modelo lineal mediante el uso de Modelos Lineales Generalizados (GLM). La estructura dependerá de la variable de respuesta, por ejemplo, si es una variable dicotómica que toma los valores 0 ó 1, no tiene sentido aplicar el modelo lineal estándar. Cuando se quiere modelar una proporción o una probabilidad en función de un conjunto de variables explicativas, puede ser conveniente aplicar una transformación logit a la variable de respuesta. La transformación logit hace que una variable entre 0 y 1 tome valores en el intervalo $(-1,+1)$ . También se puede aplicar una transformación logarítmica cuando el vínculo entre $y$ y $X$ es multiplicativo [1]. El GLM generaliza la regresión lineal al permitir que el modelo lineal se relacione con la variable de respuesta a través de una función de enlace y al permitir que la magnitud de la varianza de cada medición sea una función de su valor predicho.

Es importante tener presente que no siempre la relación entre $X$ y $E(y|X)$ se puede modelar mediante un modelo lineal con suposición de normalidad, aún después de aplicar una transformación. En este caso la clase general de modelos lineales generalizados proveen la estructura necesaria para el análisis. Así mismo los GLM se han extendido a situaciones en las que las respuestas están correlacionadas en lugar de variables aleatorias independientes [1]. Esto puede ocurrir, por ejemplo, si se trata de mediciones repetidas sobre el mismo sujeto o mediciones sobre un grupo de sujetos relacionados obtenidas, por ejemplo, de un muestreo por conglomerados [2].

Verosimilitud de los modelos lineales generalizados

Modelo normal Cuando los datos son continuos y tienen distribución normal con media

\mu

, la función de enlace del GLM es la identidad

g\left ( \mu \right )=\mu

. Por otro lado, cuando los datos son positivos se puede trabajar en una escala logarítmica. Así mismo se pueden tomar en cuenta las funciones de enlace de la distribución Gamma o Weibull cuando no se cumple la suposición de normalidad [1].

Modelo Poisson El modelo Poisson lineal generalizado se utiliza para datos de conteo, también se conoce como el modelo de regresión Poisson. La variable de respuesta

y

tiene una distribución Poisson con media y varianza

\mu

. En este caso la función de enlace es la función logarítmica y

log\mu=X\beta

[1].

$p\left ( y\mid \beta \right )=\prod_{i=1}^{n}\frac{1}{y_{i}!}e^{-exp(X\beta))}\left (exp\left ( X\beta \right )\right)^{y_{i}}$

Modelo Binomial Cuando los datos tienen una distribución binomial o Bernoulli, usualmente es de interés la proporción. Si

y_{i}\sim Bin(n_{i}, \mu_{i})

con

n_{i}

conocido, se considera como variable de respuesta a

y_{i}/n_{i}

cuya media es

\mu_{i}

. En este caso se utiliza la transformación logit como función de enlace, de manera que

g(\mu_{i}) = log(\mu_{i}/(1 − \mu_{i}))

[1].

p\left ( y\mid \beta \right )=\prod_{i=1}^{n}\binom{n_{i}}{y_{i}}\left ( \frac{e^{X\beta}}{1+e^{X\beta }} \right )^{y_{i}}\left ( \frac{1}{1+e^{X\beta }} \right )^{n_{i}-y_{i}}

Modelo multinomial logístico En este caso, la variable dependiente es el resultado de una variable multinomial, es decir, las probabilidades de ocurrencia de

y

están asociadas a variables independientes que son específicas de las alternativas, y el modelo, para la probabilidad

p_{ij}

, de que la escogencia

yi

, del sujeto i, sea j donde

y_{i}

puede ser igual a

{1,. . ., J}

[1], es igual a:

p_{ij}=\frac{exp\left ( x_{T}^{ij}\beta  \right )}{\sum_{j=1}^{J}exp\left ( x_{T}^{ij}\beta  \right )}

Para más información con relación a los modelos lineales generalizados, hay un buen material en el libro de Dobson y Barnett (2018), y en el sitio de Statmodels también hay amplia información sobre las librerías y funciones que se pueden implementar para ajustar e implementar los modelos.

CARGA DE LOS DATOS

Se cargan las librerias a implementar y los datos de registros por región que se organizaron en la sección de data cleaning. Puedes descargar el dataframe df_Region con el botón:

El entorno de desarrollo integrado (IDE) y algunos de los requisitos considerados para ejecutar los algoritmos se ilustran en los Badges, los de color verde corresponden a las bibliotecas y módulos implementados, el IDE es de color azul y el lenguaje se muestra en coral. Al hacer clic en el Badge de GitLab se puede tener acceso al repositorio con todos los códigos.

				
					# Libraries ############################################################################################################

import os
import glob
import pandas as pd
import numpy as np
from datetime import datetime

Una vez que se cargan los datos se deben tomar algunas decisiones considerando la dimensión de la matriz y el tipo de modelo que se quiere trabajar, en este caso se cuenta con 1298 registros, se tienen 16 Regiones y registros mensuales para cada región durante 6 años. El tamaño del DataFrame no es lo suficientemente grande para modelar cada Región por separado (se tienen 84 registros para cada Región, excepto AI que cuenta con 77 registros), en esté sentido, se hicieron algunos experimentos, no son los mas tradicionales ni los que suelen implementarse cuando se tienen muestras temporales pero se hicieron las pruebas para ver que se obtiene de ellos, la idea es avanzar con lo que se tiene.

Se consideraron los 1298 registros en conjunto para la construcción de un solo modelo, para ello se incorporaron las Regiones como variables ficticias y del mismo modo se incorporaron los meses como predictores. Se hicieron pruebas tratando las fechas como datos ficticios y cómo datos de intervalo, en el primer caso se sabe que no es lo ideal tratar las fechas como datos categóricos pero tampoco se quieren ignorar las fechas del muestreo en el estudio de la relación de los predictores con la variable objetivo. Se buscó sacar inferencias sobre la relación, pero ante la presencia de pocos registros no se centra la atención en el aspecto temporal. En el segundo caso, con el cual el modelo alcanzó el mejor ajuste y es el que se muestra en lo sucesivo, las fechas fueron traducidas como un predictor único que contabilizó el número de meses y años.

				
					# Se define la función que carga los datos.
def df_region_load():
    """
    Return the df.
    """
    df_Region = pd.read_parquet("./df_Region_II.parquet")
    # Se selecciona la parte de los datos con los que se quiere trabajar.
    df: DataFrame = df_Region[(df_Region['Year'] > '2014') & 
                              (df_Region['Year'] <= '2021')]
    # Variables a excluir
    df.drop(['Grupo_de_delitos_de_mayor_connotación_social',
             'Grupo_de_Infracción_a_ley_de_armas',
             'Grupo_de_Incivilidades', 'Abigeato',
             'Abusos_sexuales_y_otros_delitos_sexuales',
             'Grupo_de_Violencia_intrafamiliar',
             'Receptación',
             'Robo_frustrado',
             'Fallecidos'],
            axis=1,
            inplace=True)
    df.reset_index(drop=True)
    # Se construyen variables ficticias a partir del ID Región
    df = pd.get_dummies(df,
                        columns=['Region'])
    # Se traducen las fechas como variables de intervalo
    df[['Year', 'Month']] = df[['Year',
                                'Month']].astype(int)
    return df
# Se cargan los datos y los llamamos df_sample
df_sample = df_region_load()

MATRIZ DE CORRELACIÓN

El objetivo de examinar la matriz de correlación es comprender si hay o no relaciones entre el número de lesionados $(y)$ y los atributos que se encuentran en el dataframe (X). Se consideraron 33 variables para examinar la correlación, se trazaron los datos de la correlación como una matriz codificada por colores, las cuales se muestran en la Figura 1.

				
					# Parametros del gráfico
params = {'axes.titlesize':'10',
          'xtick.labelsize':'10',
          'ytick.labelsize':'10',
          'xtick.color':'#222222',
          'ytick.color':'#222222',
          'figure.figsize': (15,8)
          }
plt.style.use('ggplot')
plt.rcParams.update(params)
plt.figure(facecolor='#F4F4F2',
           alpha=0.8)
# Gráfico de las correlaciones
sns.heatmap(df_sample.corr(method='spearman'),
            cmap="Pastel1",
            annot=True)
# Se guarda el gráfico en la carpeta del proyecto
plt.savefig('./Corr.png', bbox_inches='tight')
plt.show()

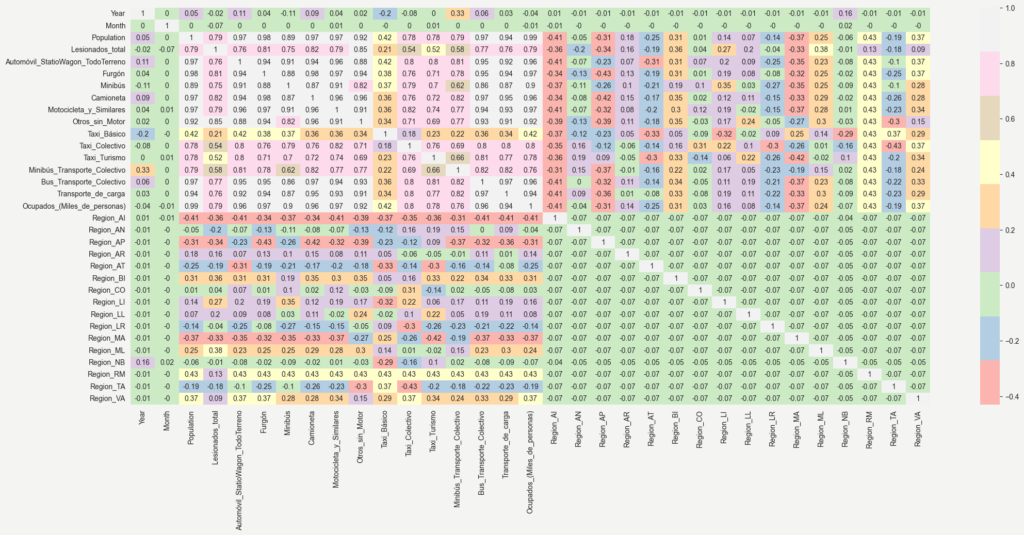
Figura 1. Mapa de calor de las correlaciones de Spearman presentes en el dataframe.

Figura 2. Lesionados de transito por mes desde el año 2015, según Región, Tasa de desocupación y población, la dimensión del punto es proporcional al tamaño poblacional.

Si se considera como variable objetivo a los Lesionados al mes en accidentes de transito (“Lesionados_total”), conviene explorar cuales son las variables que podrían explicarla con mayor fuerza. Al observar el mapa de calor (Figura 1), se identifican algunos posibles predictores que se encuentran altamente correlacionadas con la misma. Por otro lado se consideró retirar del estudio aquellos predictores que presentan una alta multicolinealidad para procurar la mayor parsimonía posible, conservando los de la flota de vehículos ya que resulta interesante observar la participación que pueden tener los diferentes vehículos en el modelo.

				
					# Se eliminan algunas de las variables que presentan alta multicolinealidad,
# especificamente las de otro contexto. 
df_sample.drop([Reg_Empresas_Sociedades',
                'Consumo_Hogares_IPSFL',
                'Fuerza_de_trabajo_(Miles_de_personas)',
                'PIB',
                'Tasa_de_desocupación_(%)',
                'Population'],
               axis=1, 
               inplace=True)

NORMALIZACIÓN

Primero se aplican las transformaciones que pudieran hacer más optimo el desempeño del modelo. En este caso se utilizo la raíz cuadrada $\sqrt{y}$ a la variable objetivo “Lesiones_total”. La transformación de raíz cuadrada tiene un efecto sustancial en la forma de la distribución, se suele utilizar para reducir la asimetría a la derecha y tiene la ventaja de que se puede aplicar a valores cero, en el caso de las lesiones hay algunos valores cero por lo que resulto conveniente su uso en lugar del logaritmo.

				
					# Transformación de raíz cúbica a la variable objetivo
df_sample['Lesionados_total'] = ((df_sample['Lesionados_total'])**(1/2)).astype('float32')

Luego de aplicar la transformación $\sqrt{y}$ se hace el reescalado de todo el dataframe o la normalización min-max, también se conoce como el min-max scaling, esté es uno de los métodos más simples para escalar el rango de cada una de los predictores y de la variable objetivo, se escala el rango, en nuestro caso, en el intervalo [0, 1]. La fórmula generalse expresa como:

$x’ = \frac{x-Min(x)}{Max(x)-Min(x)}$

				
					# Normalización de variables en el dataframe (min-max scaling).
def normalization(data_in: DataFrame = input,
                  inverse: bool = False,
                  scale_factor: list = None):
    """
    data_in: variable a normalizar
    inverse: True en caso de devolver la transformación
    return: variable normalizada
    """
    if scale_factor is None:
        scale_factor = [1, 1]
    if not inverse:
        scale_factor_: ndarray | int | float = np.max(np.abs(data_in))
        scale_factor_2 = np.min(np.abs(data_in))
        data_out = (data_in - scale_factor_2) / (scale_factor_ - scale_factor_2)
        scale_factor_ = [scale_factor_, scale_factor_2]
    else:
        data_out = (data_in * (scale_factor[0] - scale_factor[1])) + scale_factor[1]
        scale_factor_ = scale_factor
    return data_out, scale_factor_
# Se crea el dataframe normalizado (df_norm) y se cargan los parámetros de normalización
# por variable (scale_factor).
df_norm, scale_factor_ = normalization(df)

Entre los primeros pasos para ajustar el modelo se encuentra la definión del criterio para estimar de la bondad del ajuste del mismo, es conveniente implementar técnicas que permitan reducir la posibilidad de sobreajuste del modelo, por ello se utiliza la validación cruzada, en esté proceso los datos se dividen aleatoriamente en muestras de prueba y de entrenamiento. Se construye un modelo usando la muestra de entrenamiento y los errores de predicción se estiman usando la muestra de prueba. En este sentido, luego de normalizar los datos se segmentan en conjuntos de entrenamiento y prueba para validar los resultados del modelo, la segmentación se hace en una proporción de 80% de los registros para entrenar el modelo y un 20% de los registros para pronósticar.

				
					# Se identifica quien es el predictor (X) y la variable objetivo (Y)
X = pd.DataFrame(df_norm.drop('Lesionados_total',axis=1))
Y = pd.DataFrame(df_norm['Lesionados_total'])

# Se segmentan los datos normalizados en conjuntos de entrenamiento y prueba
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.20)
# Se imprimen las dimensiones de cada segmento
print('Dimensión de X_train:', X_train.shape)
print('Dimensión de X_test:', X_test.shape)
print('Dimensión de Y_train:', Y_train.shape)
print('Dimensión de Y_test:', Y_test.shape)

				
					Dimensión de X_train: (1034, 32)
Dimensión de X_test: (259, 32)
Dimensión de Y_train: (1034, 1)
Dimensión de Y_test: (259, 1)

AJUSTE DEL MODELO

El siguiente paso es ajustar el GLM, el mismo se realizó iniciando con una función de enlace Gaussiana. Luego, a efecto de procurar la parsimonia del modelo y la facilidad de implementación del mismo, se realizó un proceso iterativo para encontrar el conjunto más pequeño de variables que brinde buenas predicciones para el número de lesionados al mes por accidentes de transito. En esté sentido, se consideró eliminar los predictores no signicativos, el proceso de eliminación se realizó de uno a uno, iniciando con el predictor menos significativo, esto se debe a que un predictor puede o no cambiar su importancia en el modelo según la ausencia o presencia de otro predictor. Para lograrlo se define una función (remove_predictor) que remueve los predictores según su p-valor y luego se vuelve a realizar el ajuste del modelo sin la variable eliminada.

				
					
def remove_predictor(df: DataFrame, results: GLMResultsWrapper) -> DataFrame:
    """
    :param df: Dataframe de predictores.
    :param results: List de valores max y min por variable.
    :return: Dataframe con predictores más significativos.
    """
    # Se busca el máximo p-valor en el diccionario:
    max_p_value = max(results.pvalues.iteritems(), key=operator.itemgetter(1))[0]
    # Se elimina el predictor del dataframe:
    df.drop(columns=max_p_value, inplace=True)
    return df


def glm_model(X_train: DataFrame,
              Y_train: DataFrame,
              family: object = Gaussian()):
    """
    :param Y_train: Variable objetivo.
    :param X_train: DataFrame de todos los predictores para el train.
    :param family: distribución de enlace.
    :return: Modelo Lineal Generalizado y dataframes de predictores significativos para train y test.
    """

    insignificant_predictor = True
    # Se añade la constante a la matriz de predictores.
    X_train_glm = sm.add_constant(X_train, prepend=True, has_constant='add')
    global model
    while insignificant_predictor:
        # Sintaxis del Modelo Lineal Generalizado.
        model = sm.GLM(Y_train, X_train_glm, family=family)
        results = model.fit()
        # Se identifica el p_valor significativo (0.01, 0.05 ó 0.1).
        significant = [p_value < 0.05 for p_value in results.pvalues]
        if all(significant):
            insignificant_predictor = False
        else:
            # Cuando solo queda 1 variable no significativa.
            if X_train_glm.shape[1] == 1:
                print('No significant features found')
                results = None
                insignificant_predictor = False
            else:
                X_train_glm = remove_predictor(X_train_glm, results)
    return model.fit(), X_train_glm

#Se ajusta el modelo y calculan los valores ajustados (Y_hat) y predichos (Y_fore)
Adjust, X_train_glm, X_test_glm  = glm_model(X_train, Y_train, X_test, Gaussian())
print(Adjust.summary())
Y_hat = Adjust.predict(X_train_glm)
Y_fore = Adjust.predict(X_test_glm)

				
					                 Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:       Lesionados_total   No. Observations:                 1034
Model:                            GLM   Df Residuals:                     1012
Model Family:                Gaussian   Df Model:                           21
Link Function:               identity   Scale:                       0.0061092
Method:                          IRLS   Log-Likelihood:                 1179.6
Date:                Tue, 28 Feb 2023   Deviance:                       6.1825
Time:                        10:25:02   Pearson chi2:                     6.18
No. Iterations:                     3   Pseudo R-squ. (CS):             0.9965
Covariance Type:            nonrobust                                         
================================================================================================
                                   coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------------------------
const                            0.4446      0.016     27.951      0.000       0.413       0.476
Year                            -0.0260      0.009     -2.844      0.004      -0.044      -0.008
Month                           -0.0458      0.008     -5.856      0.000      -0.061      -0.030
Furgón                          -3.1712      0.397     -7.978      0.000      -3.950      -2.392
Camioneta                        2.1718      0.119     18.304      0.000       1.939       2.404
Motocicleta_y_Similares          1.2691      0.272      4.666      0.000       0.736       1.802
Taxi_Colectivo                  -1.1596      0.110    -10.513      0.000      -1.376      -0.943
Taxi_Turismo                     0.5962      0.122      4.887      0.000       0.357       0.835
Minibús_Transporte_Colectivo    -0.1541      0.059     -2.614      0.009      -0.270      -0.039
Bus_Transporte_Colectivo        -0.8631      0.173     -4.995      0.000      -1.202      -0.524
Ocupados_(Miles_de_personas)     1.5116      0.216      6.987      0.000       1.088       1.936
Region_AI                       -0.2744      0.018    -15.647      0.000      -0.309      -0.240
Region_AP                       -0.1181      0.015     -7.837      0.000      -0.148      -0.089
Region_BI                        0.1447      0.024      6.088      0.000       0.098       0.191
Region_CO                        0.1401      0.025      5.614      0.000       0.091       0.189
Region_LI                        0.2724      0.017     15.851      0.000       0.239       0.306
Region_LL                        0.1445      0.014     10.142      0.000       0.117       0.172
Region_MA                       -0.1609      0.014    -11.286      0.000      -0.189      -0.133
Region_ML                        0.1569      0.019      8.248      0.000       0.120       0.194
Region_NB                       -0.1406      0.022     -6.376      0.000      -0.184      -0.097
Region_TA                       -0.1681      0.019     -8.731      0.000      -0.206      -0.130
Region_VA                        0.5464      0.048     11.461      0.000       0.453       0.640
================================================================================================

				
					# Se calcula la inversa de la normalización
y_out, param  = normalization(Y_hat, inverse=True,  scale_factor=[scale_factor_[0][2],scale_factor_[1][2]])
Y_test_out, param = normalization((Y_train), inverse=True,  scale_factor=[scale_factor_[0][2],scale_factor_[1][2]])

# Se grafican los valores ajustados versus observados
def serie_plot(target: ndarray | DataFrame,
               output: ndarray | DataFrame,
               x_name: str = 'Muestra de Casos',
               y_name: str = 'Lesionados al mes',
               label_1: str = 'Observados',
               label_2: str = 'Ajustados',
               save: bool = True,
               name_save: str = 'GLM_Adjust'):
    params = {'axes.titlesize': '26',
              'xtick.labelsize': '24',
              'ytick.labelsize': '24',
              'xtick.color': '#222222',
              'ytick.color': '#222222',
              'figure.figsize': (20, 8)
              }
    plt.style.use('ggplot')
    plt.rcParams.update(params)
    plt.figure(facecolor='#E7E7E7', alpha=0.8)
    ax = plt.axes()
    plt.plot(target, color='#222222', label=label_1)
    plt.plot(output, color='#B7D1DA', label=label_2)
    plt.ylabel(y_name, size=24, color='#222222')
    plt.xlabel(x_name, size=24, color='#222222')
    plt.legend(loc='best', fontsize=18)
    ax.set_facecolor("darkgray")
    plt.title('')
    if save:
        plt.savefig('./Plot_%s.png' % name_save, bbox_inches='tight')
    else:
        pass
    plt.show()

# Se elevan al cuadrado los dataframe debido a la transformación de raíz cúbica inicial    
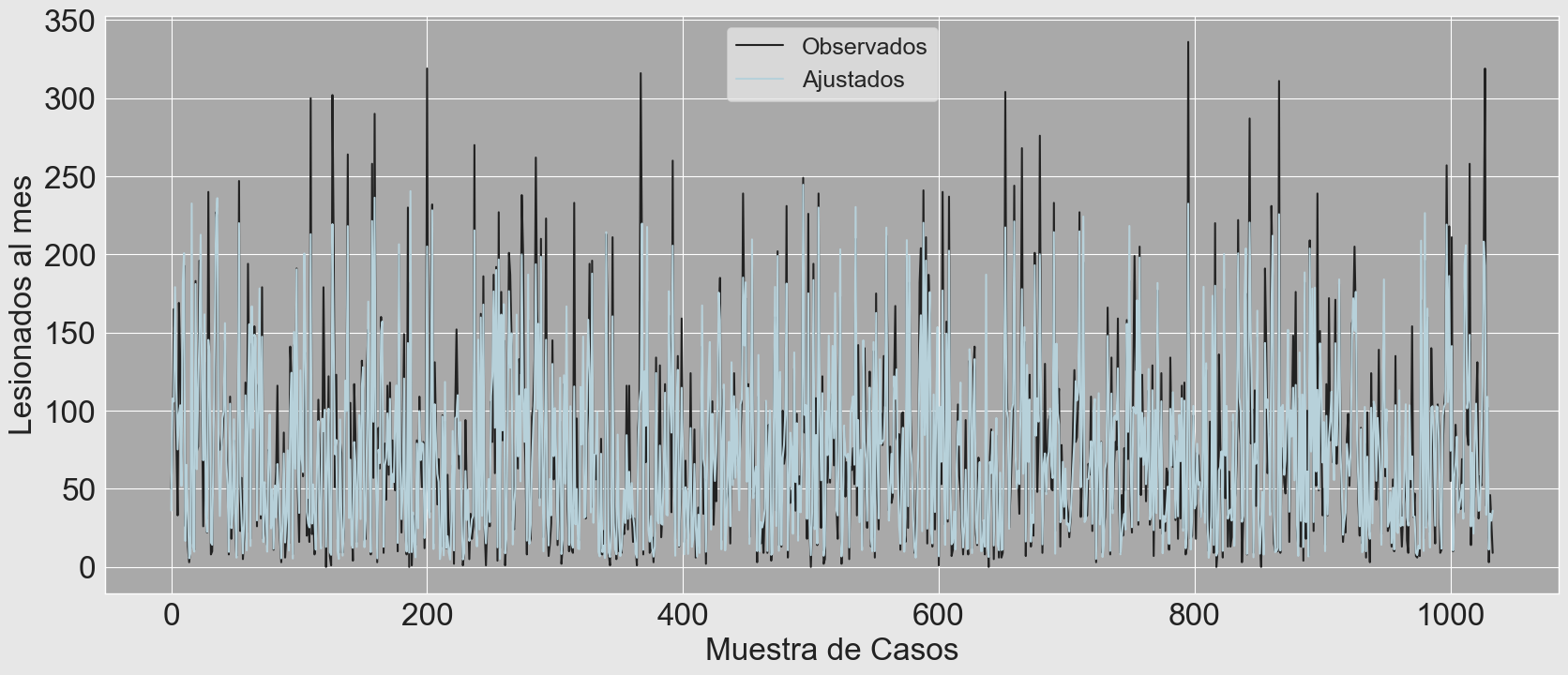
serie_plot((Y_test_out.values)**2,(y_out.values)**2)

Cuando se grafican los valores observados versus ajustados, se puede observar que el modelo si bien logra explicar buena pate de la variabilidad de la muestra de de lesioniados al mes, tiene dificultades para ajustar los valores máximos, tiende a subestimar las cifras en estos casos y ello afectará la normalidad en la validación de los residuos ya que probablemente exista un ligero sesgo negativo de la curva de normalidad (simetria negativa) o se vea la cola de la distribución más alargada de lo deseado en el lado izquierdo.

SUPUESTOS DEL MODELO

Se está ajustando un modelo lineal generalizado con función de enlace gaussiana, entonces una de las comprobaciones estándar es asegurarse de que los residuos tengan una distribución aproximadamente normal. En este sentido, la prueba de Shapiro-Wilk es unas de las más populares para probar la normalidad. Se tiene la siguiente hipótesis:

$H_{0}: e_{i}\sim N$

En Python, se usa scipy.stats.shapiro() para contrastar hipotesis de normalidad. Se puede observar que los residuos no se distribuyen normalmente ya que se rechaza la hipótesis nula. Tomando alfa como 0.05, los valores p calculados de la prueba de Shapiro-Wilk son menores que alfa. A continuación se muestra el comando para obtener el test de normalidad de Shapiro – Wilk.

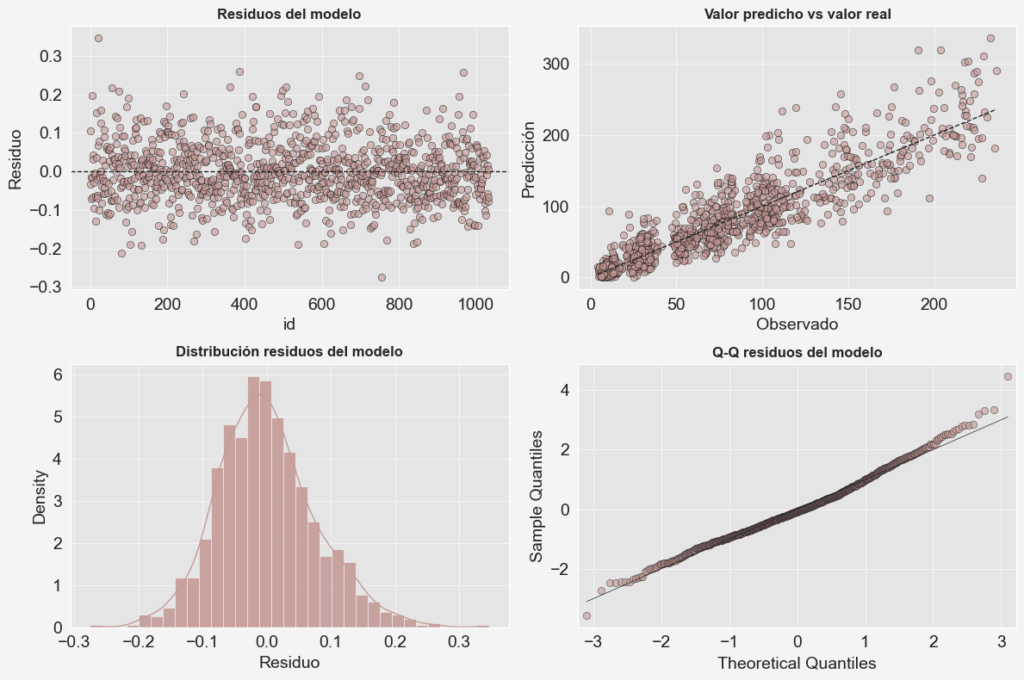
El resultado del test indica que los residuos no se distribuyen de manera normal, por lo que conviene observar un poco el histograma de la distribución de los residuos del modelo y el gráfico de comparación con los cuantiles teóricos.

				
					
#Prueba de normalidad de Shapiro-Wilk
k2, p = stats.shapiro(Adjust.resid_response.values)
alpha = 0.05
print('Null hypothesis: Residuals comes from a normal distribution')
if p < alpha:
    print("The null hypothesis can be rejected,", "p = {:g}".format(p))
else:
    print("The null hypothesis cannot be rejected,", "p = {:g}".format(p))

				
					Null hypothesis: Residuals comes from a normal distribution
The null hypothesis can be rejected, p = 3.289e-06

Si se observan las gráficas de los residuos se percibe una pequeña asimetria en la distribución de los mismos pero nada muy grave, se pudieran eliminar algunos valores extremos para tratar de alcanzar un mayor ajuste a la normalidad en los residuos

PREDICCIONES DEL MODELO

Se hicieron algunas predicciones con el modelo para ver que tan bien está funcionando en términos de inferencia.

				
					name_save = 'Residuos'
# Configuración general de los parámetros del gráfico
params = {'axes.titlesize': '12',
          'xtick.labelsize': '14',
          'ytick.labelsize': '14',
          'axes.labelsize': '14',
          'axes.labelcolor': '#222222',
          'xtick.color': '#222222',
          'ytick.color': '#222222',
          'grid.color': '#F4F4F4',
          'figure.facecolor': 'F4F4F4',
          'figure.figsize': (12, 8)
          }
plt.style.use('ggplot')
plt.rcParams.update(params)
fig, axes = plt.subplots(nrows=2,
                         ncols=2)
# Gráfico de residuos del modelo
axes[0, 0].scatter(list(range(len(y_train))), Adjust.resid_response.values,
                edgecolors=(0, 0, 0), alpha = 0.6, color='#C49B97')
axes[0, 0].axhline(y = 0, linestyle = '--', color = '#222222', lw=1)
axes[0, 0].set_title('Residuos del modelo', fontweight = "bold")
axes[0, 0].set_xlabel('id', size=14, color='#222222')
axes[0, 0].set_ylabel('Residuo', size=14, color='#222222')

# Gráfico de Distribución de los residuos del modelo
sns.histplot(data= Adjust.resid_response.values,
             color='#C49B97',
             stat= "density",
             kde= True,
             line_kws= {'linewidth': 1},
             alpha= 0.9,
             ax= axes[1, 0]
)
axes[1, 0].set_title('Distribución residuos del modelo',
                  fontweight = "bold")
axes[1, 0].set_xlabel("Residuo", size=14, color='#222222')
# Gráfico de Q-Q
sm.qqplot(
    Adjust.resid_response.values,
    fit=True,
    line='r',
    ax=axes[1, 1],
    color='#222222',
    alpha=0.6,
    dist= stats.norm,
    markeredgecolor='#222222',
    markerfacecolor='#C49B97',
    markeredgewidth = 0.5,
    fmt='b',
)
axes[1, 1].get_lines()[1].set_color("#222222")
axes[1, 1].get_lines()[1].set_linewidth("0.5")
axes[1, 1].set_title('Q-Q residuos del modelo', fontweight = "bold")

# Gráfico de Residuos versus valores predichos
axes[0, 1].scatter(y_train, prediccion_train,
                   edgecolors=(0, 0, 0),
                   alpha = 0.6,
                   color = '#C49B97')
axes[0, 1].plot([y_train.min(), y_train.max()], [y_train.min(), y_train.max()],
              'k--', color = '#222222', lw=1)
axes[0, 1].set_title('Valor predicho vs valor real', fontweight = "bold")
axes[0, 1].set_xlabel('Observado', color='#222222')
axes[0, 1].set_ylabel('Predicción', color='#222222')


fig.tight_layout()
fig.savefig('./Plot_%s.png' % name_save, bbox_inches='tight')
plt.show()

				
					# Calculo de las predicciones para el conjunto de testing
X_test['const']=1
X_test_glm = X_test[list(X_train_glm.columns)] 
Y_fore = Adjust.predict(X_test_glm)
# Inversa de la normalización inicial
y_out, param  = normalization(Y_fore, inverse=True,  scale_factor=[scale_factor_[0][2],scale_factor_[1][2]])
Y_test_out, param = normalization((Y_test), inverse=True,  scale_factor=[scale_factor_[0][2],scale_factor_[1][2]])
# Inversa de la transformación de raís cuadrada
y_test = ((y_out.values))**(2)
prediccion_test = ((Y_test_out.values))**(2)
# Gráfico de valores observados en el conjunto de prueba versus los predichos por el modelo
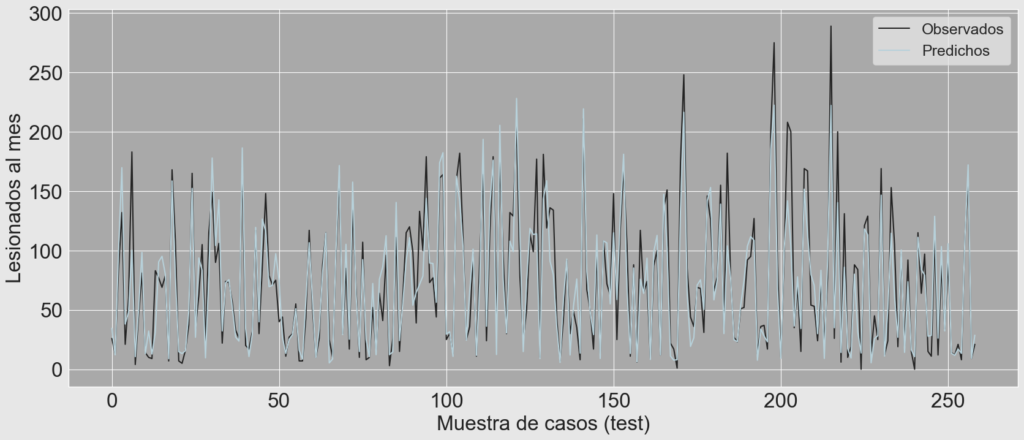
serie_plot(prediccion_test,
           y_test,
           label_1='Observados',
           label_2='Predichos',
           name_save='Predichos',
           x_name='Muestra de casos (test)')

El gráfico de valores observados versus valores predichos se muestra a continuación, como era de esperarse, el modelo tiende a ajustar bien la mayoria de los casos por debajo de los 150 lesionados pero tiende a fallar en los valores extremos a la derecha de la distribución, se intento corregir el inconveniente replicando el GLM con una función de enlace Gamma() pero no solucionó por completo el inconveniente, quizás sea preciso hacer segmentar la muestra y luego implementar una regresión por segmentación.

INDICADORES DE DESEMPEÑO

Existen diversos indicadores clave de desempeño, conocidos también por su acrónimo en inglés como KPI (Key Performance Indicator), que se pueden implementar para evaluar el comportamiento de un modelo predictivo, en el sitio de scikit-learn hay una amplia descripción sobre las técnicas de medición del desempeño de los modelos dependiendo del propósito (clasificación, clasificación multi-etiqueta, regresión y agrupación). En el ejemplo de la previsión de lesionados al mes se implementaron algunas de las métricas de desempeño para la regresión.

El primer paso fue organizar un poco las salidas en un solo DataFrame, luego se calcularon los indicadores:

				
					# Organización de los resultados en un dataframe
Train = pd.concat([pd.DataFrame(model.data.row_labels.values),
                   pd.DataFrame(y_train),
                   pd.DataFrame(prediccion_train)],axis=1)
Train.columns = ['Region', 'y', 'y_hat']
Train['Set'] = 'Train'
Test = pd.concat([pd.DataFrame(Y_test.index.values),
                   pd.DataFrame(y_test),
                   pd.DataFrame(prediccion_test)],axis=1)
Test.columns = ['Region', 'y', 'y_hat']
Test['Set'] = 'Test'

Result = pd.concat([Train,Test])

N°	Region	y	y_hat	Set
0	AT	20.000001	28.594072	Train
1	AR	64.000000	82.547670	Train
2	LR	41.999998	52.571122	Train
...	...	...	...	...
256	AN	25.000000	33.426914	Test
257	LR	54.000000	56.049842	Test
258	AN	19.000002	22.211220	Test

				
					# Calculo de los indicadores de desempeño.
def API_GLM():
    API_set = []
    API_Region = []
    for s in Result.Set.unique():
        R2 = sklearn.metrics.r2_score(
            Result[(Result['Set']== s)]['y'],
            Result[(Result['Set']== s)]['y_hat'])
        MSE = sklearn.metrics.mean_squared_error(
            Result[(Result['Set']== s)]['y'],
            Result[(Result['Set']== s)]['y_hat'])
        MAE = sklearn.metrics.mean_absolute_error(
            Result[(Result['Set']== s)]['y'],
            Result[(Result['Set']== s)]['y_hat'])
        API_set.append([s, R2, MSE, MAE])
        for i in Result.Region.unique():
            R2 = sklearn.metrics.r2_score(
                Result.query("Region == @i and Set ==  @s")['y'],
                Result.query("Region == @i and Set ==  @s")['y_hat'])
            MSE = sklearn.metrics.mean_squared_error(
                Result.query("Region == @i and Set ==  @s")['y'],
                Result.query("Region == @i and Set ==  @s")['y_hat'])
            MAE = sklearn.metrics.mean_absolute_error(
                Result.query("Region == @i and Set ==  @s")['y'],
                Result.query("Region == @i and Set ==  @s")['y_hat'])
            API_Region.append([i, s, R2, MSE, MAE])
    API_set = pd.DataFrame(API_set, columns=['Set', 'R2', 'MSE', 'MAE'])
    API_Region = pd.DataFrame(API_Region, columns=['Region', 'Set', 'R2', 'MSE', 'MAE'])
    return API_set, API_Region
# Se obtienen los indicadores
API_set, API_Region = API_GLM()

Primero se observan los indicadores de desempeño generales, se obseva un buen coeficiente de dterminación (R2) tanto en la fase de ajuste del modelo como en la fase de implementación (predicción), no se observan variaciones sustanciales en los indicadores de desempeño entre las distintas fases por lo que no parecen existir indicios iniciales de sobreajuste.

Set	R2	MSE	MAE
Train	0.829384	704.089228	17.930919
Test	0.806555	700.921766	18.550145

Finalmente si se desea guardar el modelo se puede utilizar el siguiente comando.

				
					from statsmodels.iolib.smpickle import load_pickle
# Guardar el modelo
Adjust.save('GLM_Gaussian.pickle')

# Leer el modelo 
Model = load_pickle("GLM_Gaussian.pickle")

REFERENCIAS

[1]

Llatas Salvador, I., Bravo De Guenni, L. y Perez Hernandez, M. (2008). Análisis De Datos Con Técnicas Bayesianas. Los Teques, Venezuela: IVIC – Instituto Venezolano de Investigaciones Científicas

[2]

Dobson, A. J., & Barnett, A. G. (2018). An introduction to generalized linear models. Chapman and Hall/CRC.

[1] Llatas Salvador, I., Bravo De Guenni, L. y Perez Hernandez, M. (2008). Análisis De Datos Con Técnicas Bayesianas. Los Teques, Venezuela: IVIC – Instituto Venezolano de Investigaciones Científicas

[2] Dobson, A. J., & Barnett, A. G. (2018). An introduction to generalized linear models. Chapman and Hall/CRC.